При проектировании металлических балок из двутавровых сечений важно обеспечить их устойчивость, иначе они могут потерять несущую способность при относительно небольших нагрузках. Ниже разберем, почему проверка на устойчивость критична для балок из двутавра.
Потеря общей устойчивости
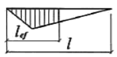
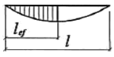
В балках при потере общей устойчивости сжатый пояс выходит из плоскости изгиба, двутавр начинает закручиваться. При этом в поясах развиваются пластические деформации, это приводит к быстрой потере несущей способности при нагрузке, не значительно превосходящей критическую.
Рисунок 1 — Потеря общей устойчивости балок
Предельное состояние для балки при потере общей устойчивости наступает раньше, чем она потеряет свою прочность. Поэтому важно обеспечить выполнение данной проверки при расчете.
При проверке общей устойчивости возникающие напряжения сравниваются с критическими:
Критические напряжения связаны с сопротивлением элемента через коэффициент φb «фи балочный» - коэффициент снижения несущей способности изгибаемого элемента из-за потери им общей устойчивости.
Формула проверки общей устойчивости изгибаемого элемента:
Формула проверки общей устойчивости изгибаемого элемента:
На величину критического напряжения и коэффициент φb влияют различные факторы:
- положение нагрузки по высоте балки: нагрузка, приложенная к верхнему поясу, увеличивает скручивание, к нижнему поясу — уменьшает его;
- форма поперечного сечения двутавра: чем шире и толще полки, тем выше критические напряжения - балка устойчивее;
- расчетная длина и расчетная схема балки (количество пролетов, консоль): критические напряжения могут быть повышены закреплением в пролете верхнего пояса балки от бокового отклонения;
- тип нагрузок (сосредоточенные или равномерно распределенные);
- марка стали по прочности: критическое напряжение для конкретного элемента одинаково вне зависимости от марки стали, а расчетные сопротивления различны.
- φ1 - коэффициент, учитывающий развитие пластических деформаций;
- Ψ - коэффициент, характеризующий влияние формы эпюры моментов;
- α - коэффициент, учитывающий геометрию сечения, расчетную длину элемента и раскрепление сжатого пояса из плоскости.
Коэффициент φb определяют с учетом влияния возможного развития пластических деформаций. Методика расчета приведена в приложении Ж, СП 16.13330.
При значении коэффициента φ1 = 0,85 критические напряжения переходят в упругопластическую фазу, из-за уменьшения модуля деформации меняется коэффициент φb. Соответственно формула определения φb зависит от условия φ1 ≤ 0.85 или φ1 > 0.85.
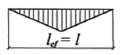
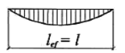
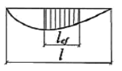
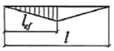
Для вычисления φb используется коэффициент Ψ, характеризующий влияние формы эпюры моментов на устойчивость плоской формы изгиба. В таблице Ж.1 СП 16.13330 приведены формы эпюр изгибающих моментов и соответствующие им значения коэффициента Ψ.
Таблица 1 — Ж.1 СП 16.13330
| Число закреплений сжатого пояса в пролете | Вид нагрузки в полете | Эпюра MX на участке lef | Пояс, к которому приложена нагрузка | Коэффициент Ψ при значениях α | |
|---|---|---|---|---|---|
| 0,1 ≤ α ≤ 40 | 40 < α ≤ 400 | ||||
| Без закреплений | Сосредоточенная |
|
Сжатый | 1,75+0,09α | 3,3+0,05α -4,5*10-5α 2 |
| Растянутый | 5,05+0,09α | 6,6+0,05α -4,5*10-5α 2 | |||
|
Сжатый | 1,60+0,08α | 3,15+0,04α -2,7*10-5α 2 | ||
| Растянутый | 3,80+0,08α | 5,35+0,04α -2,7*10-5α 2 | |||
| Два и более, делящие пролет l на равные части | Любая |
|
Любой | 2,25+0,07α | 3,6+0,04α -3,5*10-5α 2 |
| Одно в середине | Сосредоточенная в середине |
|
Любой | 1,75 γ1 | |
| Сосредоточенная в четверти |
|
Сжатый | 1,14 γ1 | ||
| Растянутый | 1,60 γ1 | ||||
| Равномерно распределенная |
|
Сжатый | 1,14 γ1 | ||
| Растянутый | 1,30 γ1 | ||||
Значения коэффициент Ψ вычислены в функции от коэффициента α при нагрузке по верхнему или нижнему поясу и для случая чистого изгиба.
Заключение
Особое внимание при вычислении φb следует уделять расчетной длине сжатого пояса, так как она может не совпадать с расчетной длиной балки из плоскости стенки.
Если при проверке балки на общую устойчивость выясняется, что условие не обеспечено, следует уменьшить расчетную длину сжатого пояса за счёт изменения схемы связей.
В случае, если верхний пояс балок раскреплен настилом, образующим жесткий диск перекрытия, можно считать, что сечение балки надежно закреплено от поворота. Необходимость проверки расчетом общей устойчивости отпадает.
