При проектировании зданий со стальным каркасом и назначении конструктивной системы покрытия выбор часто падает в сторону беспрогонных кровельных систем. Напомним, что такая система не подразумевает использования прогонов для формирования кровли — профилированный лист или кассета крепится непосредственно к поясам ферм. Такое решение показывает высокую эффективность, но требует учитывать ряд важных аспектов, среди которых:
- Организация связевой системы и работа профилированного листа в качестве горизонтальной диафрагмы жесткости;
- Выбор оптимальной схемы раскладки профлиста, а также способы его усиления в зонах образования снеговых мешков;
- Расчет узлов крепления профлиста к поясу ферм;
- Корректный учет раскрепления ферм с помощью профлиста.
В данной статье мы подробно рассмотрим вопрос корректного учета раскрепления ферм профилированным листом при расчете на устойчивость.
Особенности раскрепления верхнего пояса фермы в беспрогонных кровлях
В беспрогонных кровлях верхняя полка верхнего пояса фермы раскрепляется профилированным настилом. Полное игнорирование этого раскрепления приводит к неэффективным решениям: потребуется установка дополнительных распорок, что значительно увеличит металлоемкость конструкции и трудоемкость работ, нивелируя преимущества беспрогонной кровли относительно прогонной системы.
В то же время, считать профнастил постоянным раскреплением верхнего пояса из плоскости некорректно, поскольку центр тяжести элемента и плоскость крепления профнастила не совпадают.
Возникает вопрос: как правильно учитывать раскрепление профлистом при проверке устойчивости верхнего пояса?
Расчетное обоснование
В беспрогонных кровлях с уклоном менее 10° профилированный настил может рассматриваться как жёсткая диафрагма, при условии его крепления в каждой нижней гофре (п. 15.4.7 СП 16.13330.2017). Аналогичные требования к устройству диафрагм жёсткости из профнастила содержатся в п. 8.4.1 СТО 0043-2014. При этом крепления настила должны быть рассчитаны на восприятие поперечных усилий в горизонтальной плоскости.
Верхний пояс фермы в беспрогонной системе работает как сжато-изгибаемый элемент, так как на него действует равномерно распределённая нагрузка. Для таких элементов, подкреплённых вдоль одной из полок, возможна потеря устойчивости по изгибно-крутильной форме относительно стесненной оси (п. 7.3.5 СП 294.1325800.2017). Эта форма потери устойчивости становится особенно критичной при одновременном наличии двух факторов: использовании сечений поясов, обладающих низкой крутильной жёсткостью, и применении фасоночных узлов, имеющих недостаточную жёсткость на изгиб из плоскости фермы.
Аналитическое описание данной формы потери устойчивости представлено в [1-3]. Подходы, изложенные в указанных источниках, нашли отражение в расчетных формулах, используемых в действующих нормах проектирования. Далее на конкретном примере рассмотрим применение этих формул для проверки устойчивости элементов согласно требованиям как отечественных, так и зарубежных нормативных документов.
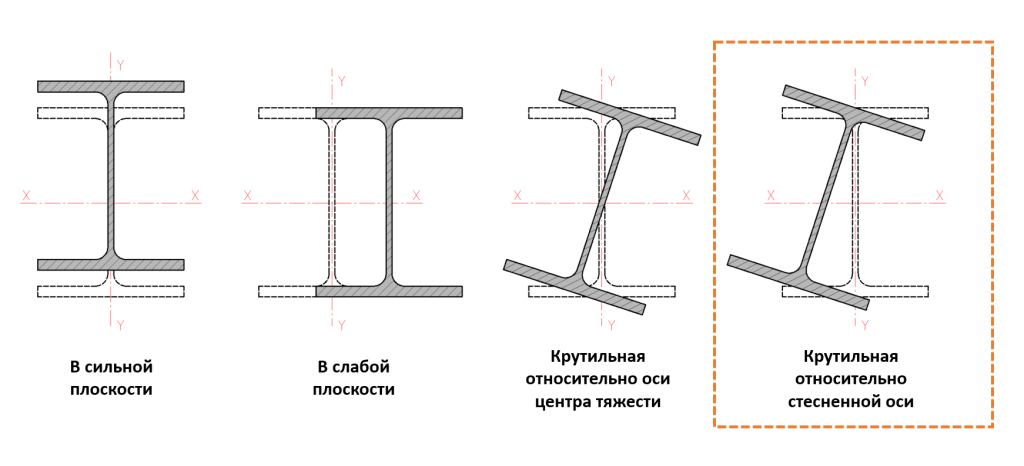Рисунок 1 — Формы потери устойчивости
Исходные данные
Рассмотрим порядок расчета на примере стропильной фермы ФС-24/5-2.4 из альбома технических решений.
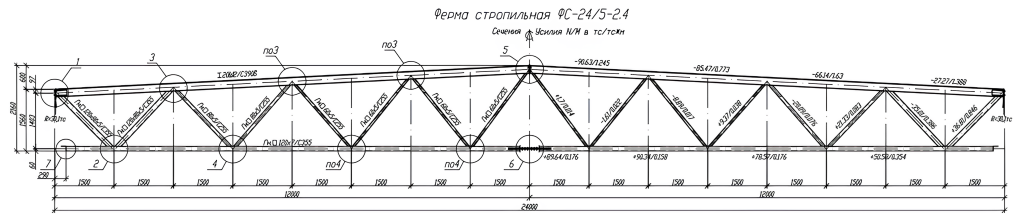Рисунок 2 — Чертеж исходной фермы
- Усилия в центральной панели верхнего пояса фермы:
- N=90.63 тс — продольная сила;
- Mx=1.245 тс*м — изгибающий момент в сильной плоскости сечения.
- Сечение верхнего пояса 20Ш2:
- A=38.8 см2 — площадь поперечного сечения;
- Ix=3502.12 см4 — момент инерции в сильной плоскости;
- Iy=661.25 см4 — момент инерции в слабой плоскости;
- ix=84.21 мм — радиус инерции в сильной плоскости;
- iy=36.59 мм — радиус инерции в слабой плоскости;
- h=199 мм — высота сечения;
- tIf=11.5 мм — толщина полки двутавра;
- bIf=151 мм — ширина полки двутавра;
- tIw=11.5 мм — толщина стенки двутавра;
- bIw=151 мм — ширина стенки двутавра.
- Сталь верхнего пояса С390Б:
- Ry=390 МПа — расчетное сопротивление;
- E=2*105 МПа — модуль упругости стали;
- G=8*104 МПа — модуль сдвига стали.
- Ly=12 м — шаг распорок по верхнему поясу фермы (отображение распорок и горизонтальных связей по верхнему поясу ферм представлено на рисунке ниже).
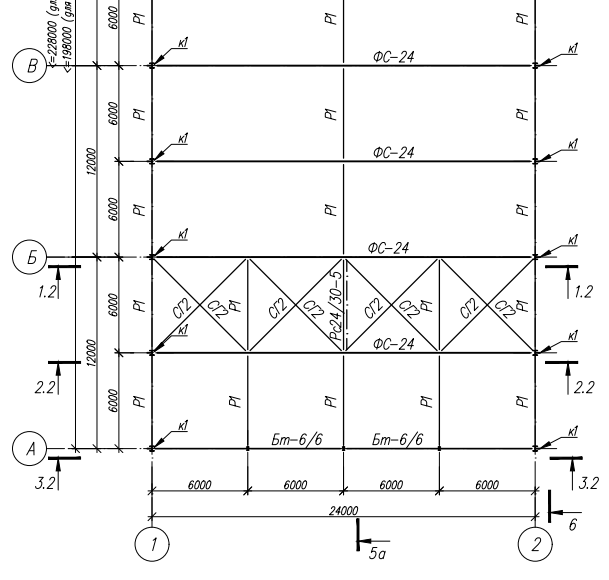Рисунок 3 — Расположение связей и распорок по верхнему поясу фермы
Пример проверки по СП
Проверка устойчивости сжато-изгибаемого двутаврового элемента, непрерывно подкрепленного вдоль одной из полок, должна выполняться в соответствии с п. 9.2.7 СП 16.13330.2017 — по формуле №111 с учётом формулы (Д.4):
\frac{N}{c_{max}\,\varphi_y\,A\,\gamma_c} < 1
Вычисление коэффициента устойчивости при центральном сжатии \varphi_y
Коэффициент устойчивости при центральном сжатии определяется согласно п. 7.1.3:
\lambda_{\text{усл}} = \frac{L_y}{i_y}\sqrt{\frac{R_y}{E}} = \frac{12000}{36.59}\sqrt{\frac{390}{2\cdot10^{5}}} = 14.482
\delta = 9.87\,(1 - \alpha_I + \beta_I \lambda_{\text{усл}}) + \lambda_{\text{усл}}^{2} = 9.87\,(1 - 0.04 + 0.09\cdot 14.482) + 14.482^{2} = 232.075
Где \alpha_I и \beta_I — коэффициенты формы сечения для двутавра по таблице 7.
\varphi_{y1} = 0.5\,\frac{\delta - \sqrt{\delta^{2}-39.48}}{\lambda_{\text{усл}}} = 0.5\,\frac{232 - \sqrt{232^{2} - 39.48}}{14.482} = 0.044
\varphi_{y2} = \frac{7.6}{\lambda_{\text{усл}}^{2}} = \frac{7.6}{14.482^{2}} = 0.036
\varphi_y = \min(\varphi_{y1},\,\varphi_{y2}) = 0.036
Вычисление коэффициента cmax
Коэффициент cmax, используемый в формуле проверки, учитывает влияние изгибающего момента на пространственную потерю устойчивости стержня и рассчитывается согласно формуле Д.4:
c_{\max} = \frac{ 1 + \frac{I_x}{I_y} + \frac{\alpha}{9.87} }{ 1 + 4\left( \frac{i_x^{2} + i_y^{2}}{h^{2}} + \frac{e_x}{h} \right) }
Для расчета cmax в первую очередь следует определить коэффициент α. Согласно Ж.4 для этого принимается коэффициент k, зависящий от раскрепления сжатого пояса в пролете: k = 1 — при отсутствии закреплений; k = 1,54 — при наличии закреплений. В нашем случае:
k = 1,54
Далее по формуле приложения Д вычислим момент инерции при свободном кручении It. У двутавровых сечений момент инерции при кручении сравнительно мал и именно поэтому проверка устойчивости изгибно-крутильной формы может являться определяющей при подборе сечения верхнего пояса фермы.
I_t = \frac{1.29}{3}\left( 2\,b_{If}\,t_{If}^{3} + b_{Iw}\,t_{Iw}^{3} \right) = 22.943\ \text{см}^4
Зная k, It, h и Ly (в формуле Д.4 указано, что его следует принимать как расстояние между распорками или связями), определим значение α по формуле Ж.3 (а) для прокатных двутавров:
\alpha = k\,\frac{I_t}{I_y} \left(\frac{L_y}{h}\right)^{2} = 1.54\,\frac{22.943}{661.25} \left(\frac{12000}{199}\right)^{2} = 194.294
Следующим шагом необходимо определить значение эксцентриситета ex. Согласно примечанию к формуле Д.4 эксцентриситет считается положительным, если точка приложения силы смещена в сторону свободной полки. В нашем случае эксцентриситет будет отрицательным:
e_x = \frac{-M_x}{N} = \frac{-1.245}{90.63} = -13.737\ \text{мм}
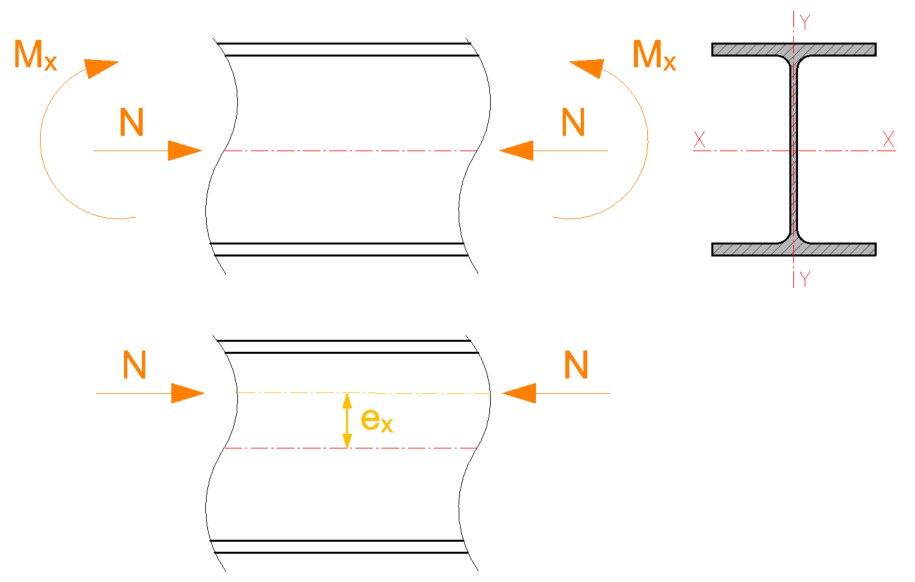Рисунок 4 — Определение эксцентриситета
В результате, подставляя все значения в формулу Д.4, вычисляем cmax:
c_{\max} = \frac{ 1 + \frac{3502.12}{661.25} + \frac{194.294}{9.87} }{ 1 + 4\left( \frac{84.21^{2} + 36.59^{2}}{199^{2}} + \frac{-13.737}{199} \right) } = 16.492
Итоговая проверка
\frac{N}{c_{\max}\,\varphi_y\,A\,\gamma_c} = \frac{90.63}{16.492 \cdot 0.036 \cdot 38.8 \cdot 390 \cdot 1} = 0.89 < 1
Пример проверки по AISC
Проверка устойчивости по изгибно-крутильной форме относительно стесненной оси изложена в C-E4-1 AISC 360-16:P_{cr} = 0.9 \cdot \frac{-2.724\,N}{A\,R_y} \cdot \ln\left(\frac{N}{A\,R_y}\right) \cdot \left( \frac{\pi^2 E I_y}{L_{cz}^2} \left(\frac{h_2}{4} + \frac{h_2}{4}\right) + G I_t \right) \cdot \frac{1}{i_x^2 + i_y^2 + \frac{h_2}{4}} = 101.61\ \text{тс}
\frac{N}{P_{cr}} = \frac{90.63}{101.61} = 0.89
Сравнение различных вариантов учета раскрепления верхнего пояса
В таблице ниже приведено сравнение различных подходов к учету раскрепления верхнего пояса ферм в беспрогонных системах. Результаты проверок показывают, что полный неучет раскрепления профнастилом приводит к чрезмерно консервативным результатам и, как следствие, к неэффективным конструктивным решениям.
При учете раскрепления профлистом проверка на устойчивость из плоскости действия момента с шагом раскрепления, равным расстоянию между креплениями профлиста, может оказаться не определяющей. Поэтому, помимо этой проверки, необходимо также выполнять расчет на устойчивость по изгибно-крутильной форме относительно стесненной оси. Из таблицы видно, что результаты расчета для этой формы потери устойчивости, полученные по AISC-360 и СП 16, согласуются между собой.
| Форма потери устойчивости | Формула проверки | Раскрепление верхнего пояса по направлению формы потери устойчивости | КИ |
|---|---|---|---|
| Из плоскости действия момента | п. 9.2.4 СП 16.13330.2017 | Распорки с шагом 12 м, раскрепление профлистом не учитывается | 352% |
| Из плоскости действия момента | п. 9.2.4 СП 16.13330.2017 | Раскрепление профлистом с шагом 0,3 м (расстояние между нижними гофрами, Рисунок 5) | 59% |
| Изгибно-крутильная относительно стесненной оси | п. 9.2.7 СП 16.13330.2017 | Распорки с шагом 12 м, учитывается раскрепление верхней полки профлистом | 89% |
| Изгибно-крутильная относительно стесненной оси | C-E4-1 AISC 360-16 | Распорки с шагом 12 м, учитывается раскрепление верхней полки профлистом | 89% |
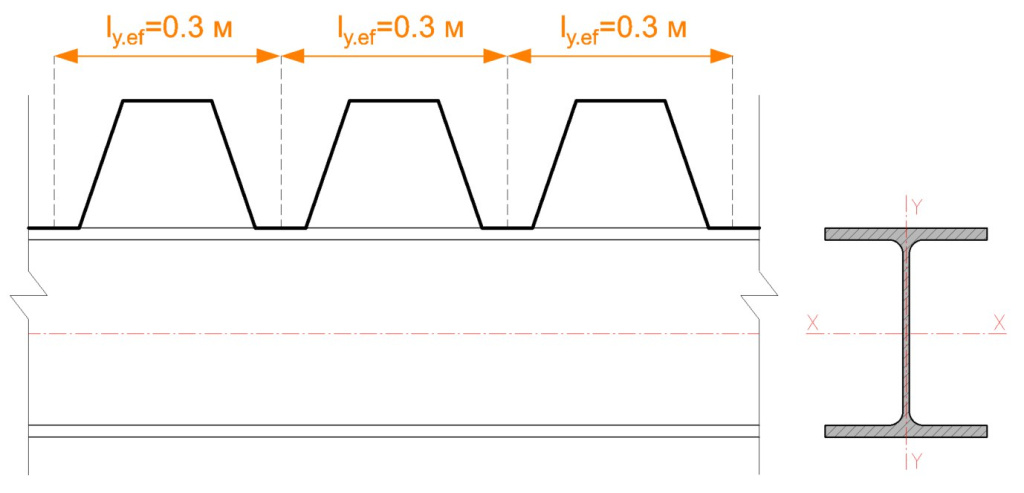Рисунок 5 — Вариант расчета раскрепления
Вывод
Учет раскрепления верхнего пояса фермы профилированным настилом в беспрогонных системах позволяет значительно сократить количество распорок, а значит — снизить металлоемкость и трудозатраты без ущерба для надежности конструкции.
Однако при учете раскрепления профлистом проверка устойчивости из плоскости действия момента может оказаться не определяющей, в особенности в случае, если верхний пояс обладает малой крутильной жесткостью (например, двутавровое сечение или спаренный уголок), а узлы крепления решетки низкой изгибной жесткостью из плоскости фермы (например, узлы на фасонках). Поэтому, помимо этой проверки, необходимо также выполнять расчет на устойчивость по изгибно-крутильной форме относительно стесненной оси согласно п. 9.2.7 СП 16.13330.2017. В качестве дополнительной проверки результатов можно воспользоваться расчетом по C-E4-1 AISC 360-16.
Источники
- Timoshenko, S.P., and Gere, J.M. (1961), Theory of Elastic Stability, 2nd Ed., McGraw-Hill, New York, N.Y. (Chapter 5. Torsional Buckling)
- Errera, S.J., and Apparao, T.V.S.R. (1976), “Design of I-Shaped Columns with Diaphragm Bracing,” Journal of the Structural Division, ASCE, Vol. 102, No. 9, pp. 1,685–1,701.
- Helwig, T., and Yura, J. (1999), “Torsional Bracing of Columns,” Journal of Structural Engineering, Vol. 125, No. 5, pp. 547–555.
