Ядро сечения — это область вокруг центра тяжести поперечного сечения элемента, в пределах которой приложенное продольное усилие вызывает в сечении напряжения одного знака. Иначе говоря, если нагрузка действует внутри ядра, то во всех точках сечения возникают либо только сжимающие, либо только растягивающие напряжения — без смены знака.
Это одно из базовых понятий в сопромате и расчетах конструкций на внецентренное сжатие.
Рисунок 1 — Эпюры нормальных напряжений при приложении сжимающей нагрузки вне, на границе и внутри ядра сечения
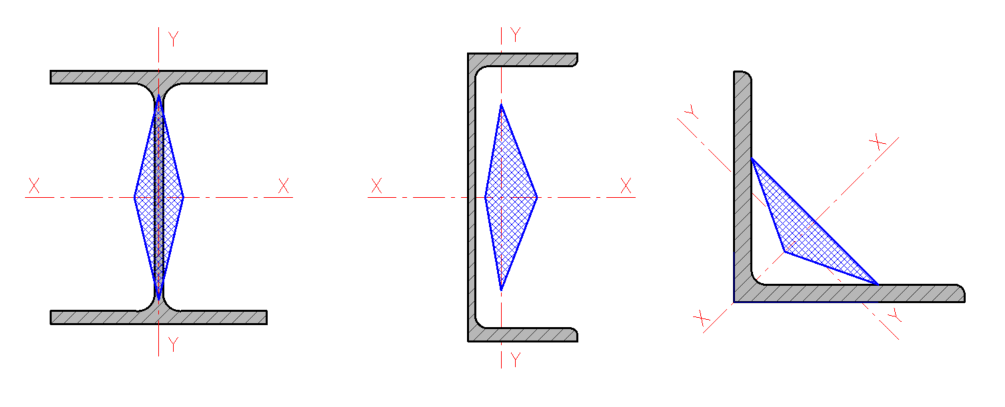Рисунок 2 — Ядро сечения для двутавра, швеллера и уголка
Для определения положения границы ядра, используют уравнение нейтральной линии сечения при внецентренном сжатии (2), которое выводится из условия нулевых напряжений (1).
- \sigma — нормальные напряжения в рассматриваемой точке сечения;
- x, y — координаты рассматриваемой точки сечения;
- N — продольная сила;
- A — площадь сечения;
- M_x, M_y — изгибающие моменты относительно осей x и y;
- I_x, I_y — осевые моменты инерции сечения относительно осей x и y.
- x_p, y_p — координаты точек приложения силы P;
- x, y — координаты точек, лежащих на нейтральной линии;
- i_x, i_y — радиусы инерции поперечного сечения.
Уравнение нейтральной линии математически является уравнением прямой, которое для удобства можно записать в отрезках:
- a — отрезок, отсекаемый прямой на оси x (точка пересечения (a,0));
- b — отрезок, отсекаемый прямой на оси y (точка пересечения (0,b)).
Отсюда можем выразить a и b (4) и определить координаты границ ядра сечения (5):
Как построить ядро сечения — алгоритм
Существует несколько способов построения ядра сечения в зависимости от формы поперечного сечения и требований к точности. На практике чаще всего используется метод касательных нейтральных линий, позволяющий получить геометрическую границу ядра без трудоёмких интегральных расчетов.
Если сила P приложена на границе ядра сечения, то соответствующая нейтральная линия касается, но не пересекает контур поперечного сечения. В таком случае алгоритм построения ядра сечения выглядит следующим образом:
- Провести касательные нейтральные линии к сечению (или к огибающей сечения)
- Для каждой касательной найти две точки пересечения с осями координат:
- Пересечение с осью x: при y=0 → x=a
- Пересечение с осью y: при x=0 → y=b
- Для каждой касательной вычислить координаты соответствующей точки (x_0,y_0) на границе ядра сечения:
x_0 = -\frac{i_y^2}{a},y_0 = -\frac{i_x^2}{b}
- Построить контур ядра сечения последовательно соединив полученные точки
Пример построения ядра сечения для круглого поперечного сечения
- Так как круглое сечение симметрично относительно любой оси, проходящей через центр, ядро сечения так же будет представлять из себя круг. В таком случае достаточно провести одну касательную 1-1.
- Точка пересечения касательной с осью y находится на расстоянии, равном радиусу окружности. Точка пересечения касательной с осью x отсутствует:
a \to \inftyb = R
- Вычисляем координаты соответствующей точки (x_0,y_0) на границе ядра сечения:
x_0 = -\frac{i_y^2}{a} = 0,y_0 = -\frac{i_x^2}{b} = -\frac{(0.5 R)^2}{R} = -\frac{R}{4}
- Строим контур ядра сечения в виде окружности, радиус ядра сечения для которой равен R/4:
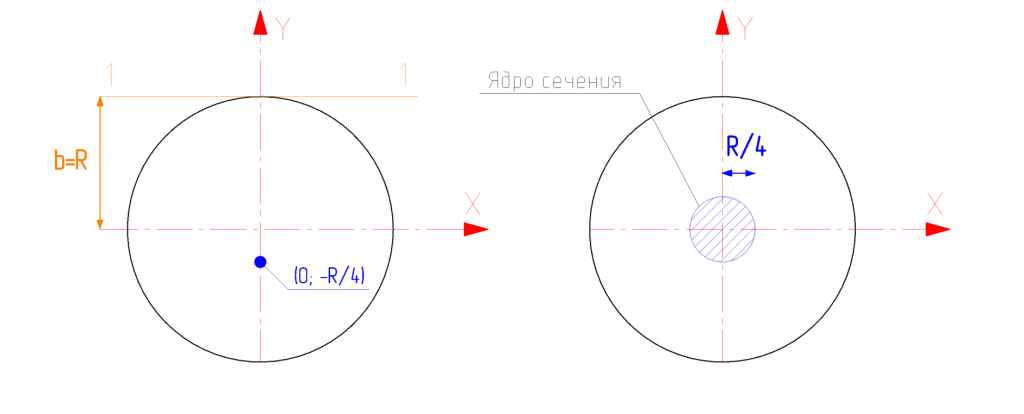Рисунок 3 — Построение ядра сечения круга
Пример построения ядра сечения для прямоугольного поперечного сечения
- Проведем касательные 1-1, 2-2, 3-3, 4-4. Так как сечение симметричное, определим точки ядра сечения для касательных 1-1 и 2-2, а для касательных 3-3 и 4-4 построим точки симметрично.
- Точка пересечения касательной 1-1 с осью y находится на расстоянии, равном половине стороны прямоугольника, точка пересечения касательной с осью x отсутствует. Точка пересечения касательной 2-2 с осью x находится на расстоянии, равном половине стороны прямоугольника, точка пересечения касательной с осью y отсутствует.
a_{(1-1)} \to \inftyb_{(1-1)} = 0,5ha_{(2-2)} = 0,5hb_{(2-2)} \to \infty
- Вычисляем координаты соответствующих точек (x_{0_{(1-1)}},y_{0_{(1-1)}}) и (x_{0_{(2-2)}},y_{0_{(2-2)}}) на границе ядра сечения:
x_{(0 (1-1))} = -\frac{i_y^2}{a} = 0,y_{(0 (1-1))} = -\frac{i_x^2}{b} = -\frac{\left(\frac{h}{\sqrt{12}}\right)^2}{0,5h} = -\frac{h}{6}x_{(0 (2-2))} = -\frac{(\frac b {\sqrt{12}})^2}{0,5b} = -\frac{b}{6},y_{(0 (2-2))} = -\frac{i_x^2}{b} = 0
- Построим контур ядра сечения в виде ромба, соединив точки:
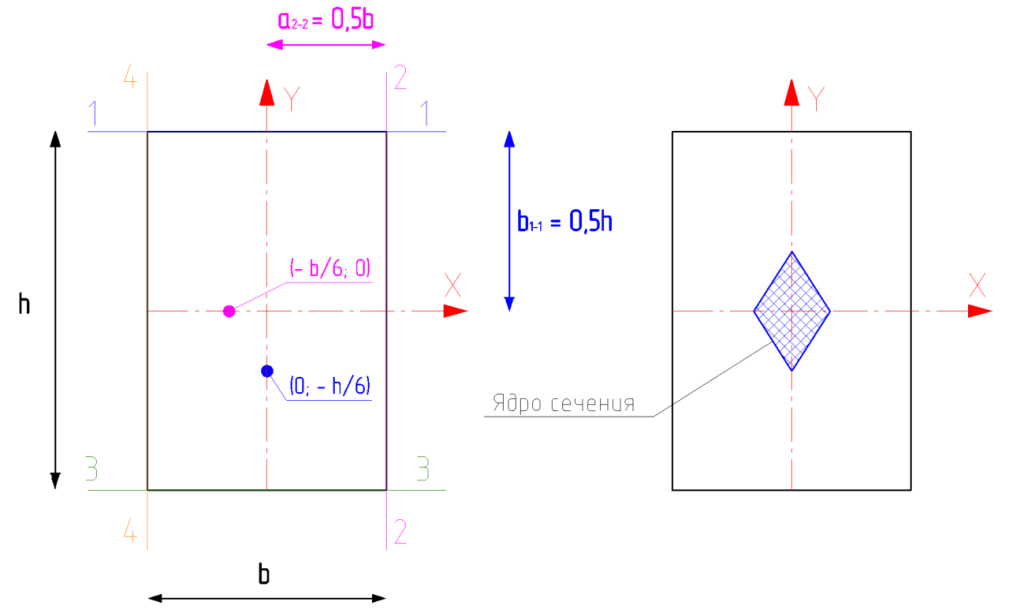Рисунок 4 — Построение ядра сечения прямоугольника
Для построения ядра сечения можно использовать конструкторы сечений или специализированные онлайн-инструменты. Эти инструменты значительно экономят время, а в их базы включены сложные профили — такие как двутавры, швеллеры, уголки, трубы и т. д.
Применение ядра сечения в инженерных расчетах
Положение ядра сечения играет важную роль в оценке влияния эксцентриситетов приложения силы на напряженно-деформированное состояние при сжатии и растяжении. Например, положение ядра сечения необходимо для определения напряжений под подошвой столбчатого фундамента (рисунок 5).
Рисунок 5 — Зоны различных эксцентриситетов столбчатых фундаментов
Примеры использования ядра сечения
| Пункт норм | Тип проверки | Формула |
|---|---|---|
| СП 22.13330.2016. п. 5.6.28 | Внецентренное сжатие фундамента, определение краевого давления |
при e \leq \frac{l}{6}:
p = \frac{N}{A} + \gamma_m \cdot d \pm \frac{M}{w}
при e > \frac{l}{6}:
P = \frac{2 \cdot (N + \gamma_m \cdot d \cdot l \cdot b)}{3 \cdot b \cdot C_0}
|
| СП 15.13330.2020 п. 7.20 | Срез неармированной кладки по неперевязанным швам и перевязанным швам кладки |
Q \leq (R_{sq} + 0.8 \cdot n \cdot \mu \cdot \sigma_0) \cdot A
При эксцентриситетах, выходящих за пределы ядра сечения:
A = A_C
|
| СП 15.13330.2020 п. 7.32 | Устойчивость внецентренно сжатых элементов с сетчатым армированием |
При малых эксцентриситетах, не выходящих за пределы ядра сечения:
N \leq m_g \cdot \phi_1 \cdot R_{skb} \cdot A_c \cdot \omega
|
