Общие данные
При проектировании балочных клеток перекрытий, составленных из главных и второстепенных балок, наиболее распространенным в инженерной практике конструктивным решением является шарнирное болтовое соединение. Указанное решение предполагает передачу вертикальных усилий на главную балку с экцентриситетом приложения силы, что вызывает в сечении главной балки крутящий момент. Большинство расчетных комплексов не позволяют выполнить оценку напряжений от крутящего момента при анализе расчетной схемы, составленной из стержневых конечных элементов, что может привести к ошибкам при подборе сечений элементов конструкции.
В отчете представлены результаты анализа влияния эксцентриситета приложения нагрузки от второстепенной балки на главную крайнюю балку перекрытия на напряженно-деформированное соостояние конструкции. Расчеты конструкций на поперечный изгиб с кручением были выполнены по методике, изложенной в книге Бычкова Д.В. “Строительная механика стержневых тонкостенных конструкций — М.: Госстройиздат, 1962.”, а также методом конечных элементов в расчетном комплексе ЛИРА 10.
Расчетные параметры конструкции
В работе были рассмотрены 2 расчетных случая: без учета эксцентриситета приложения нагрузки на главную балку; с учетом эксцентриситета и соответствующих крутящих усилий.
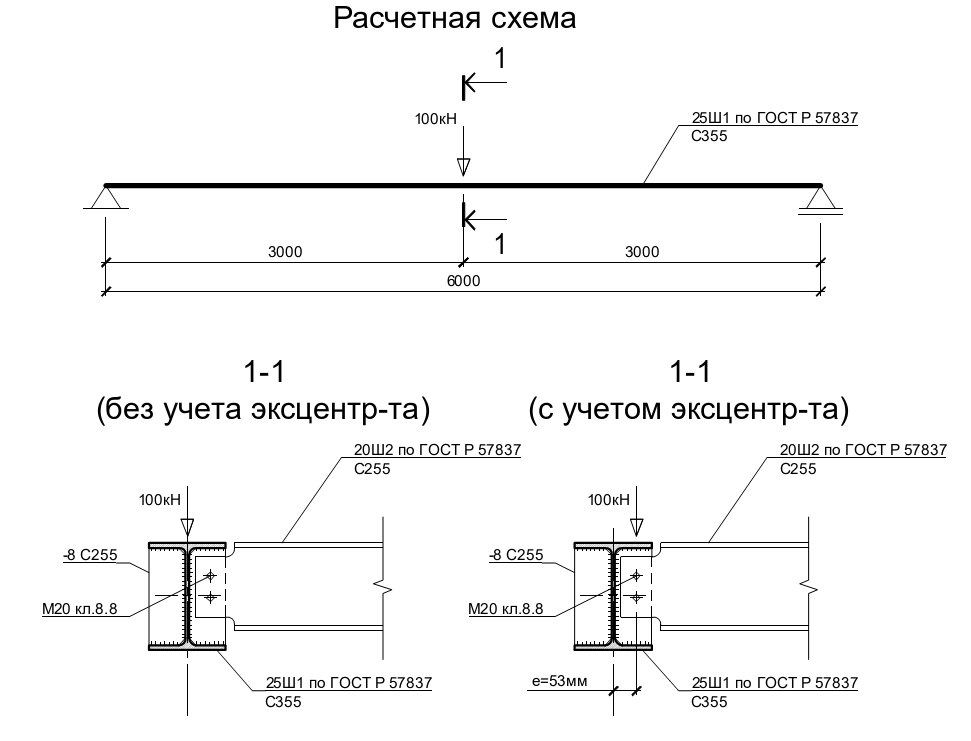Рисунок 1 — Расчетная схема и варианты приложения нагрузки
Расчет главной балки 25Ш1 без учета кручения
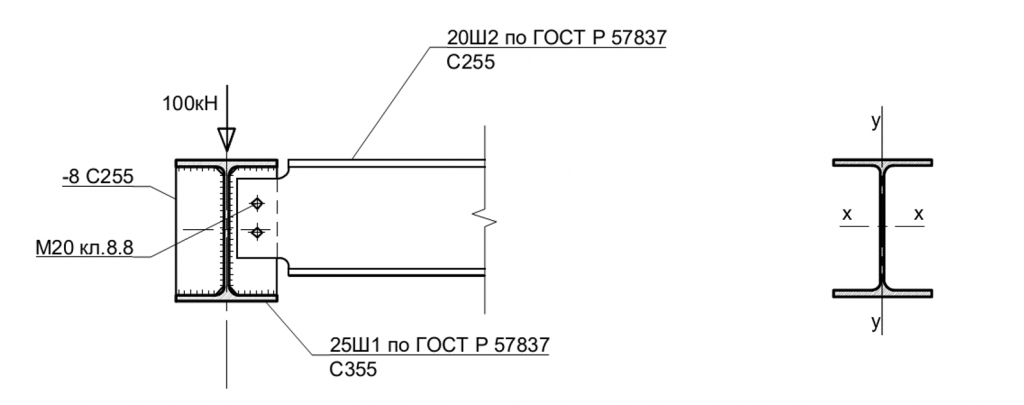Рисунок 2 — Расчетная схема без учета эксцентриситета
Геометрические и прочностные характеристики главной балки 25Ш1 при расчете на поперечный изгиб представлена в таблице ниже.
Таблица 1 — Геометрические и прочностные характеристики
| Расчетное сопротивление стали | Ry=350 МПа |
| Модуль упругости стали | Est=206 000 МПа |
| Момент сопротивления сечения относительно оси х | Wx=501 700 мм3 |
Расчет на изгиб выполняется по прочности в предположении сплошного раскрепления верхнего пояса балки.
Расчетный изгибающий момент определяется по правилам теории сопротивления материалов для шарнирно-опертой балки от действия точечной нагрузки в середине пролета:
Для проверки условия прочности определим максимальное расчетное напряжение в сечении балки по п.8.2.1 СП16.13330.2017:
Расчетное напряжение не превышает расчетного сопротивления стали.
Сечение балки подобрано с коэффициентом использования 0.85.
Проверка результатов ручного расчета на поперечный изгиб методом конечных элементов в программе ЛИРА 10.
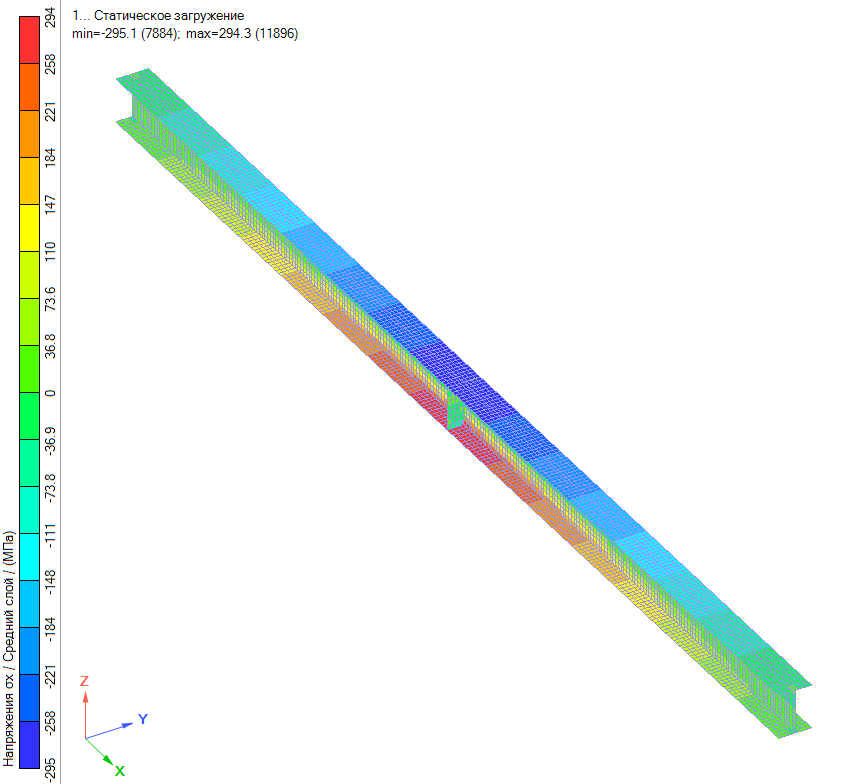Рисунок 3 — Максимальные главные расчетные напряжения в балке 25Ш1
Максимальное напряжение в сечении балки:
Сравнение результатов ручного расчета и расчета в программе ЛИРА 10:
Расчет главной балки 25Ш1 с учетом кручения
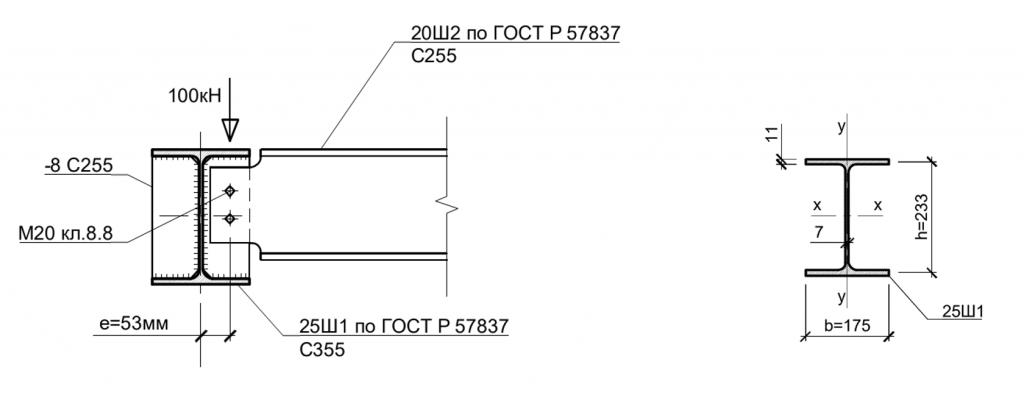Рисунок 4 — Расчетная схема с учетом эксцентриситета
Геометрические и прочностные характеристики главной балки 25Ш1 при расчете на поперечный изгиб с кручением представлена в таблице ниже.
Таблица 2 — Геометрические и прочностные характеристики
| Расчетное сопротивление стали | Ry=350 МПа |
| Модуль упругости стали | Est=206 000 МПа |
| Модуль сдвига стали | G=80 000 МПа |
| Момент сопротивления сечения относительно оси х | Wx=501 700 мм3 |
| Момент инерции сечения относительно оси y | Jy=9 844 800 мм4 |
| Момент инерции при кручении | Jt=234 681 мм4 |
| Секториальный момент инерции | Jω=133 616 086 800 мм6 |
| Изгибо-крутильная характеристика сечения | K=0.000 826 мм-1 |
| Секториальная координата наиболее удаленной точки | ωf=10 194 мм2 |
Ниже приведены подробные вычисления расчетных характеристик сечения балки.
Момент инерции при кручении (формула 7 [1]):
bi и ti — ширина и толщина поясов и стенки двутавра соответственно
k=1.29 – поправочный коэффициент для двутаврового сечения с двумя осями симметрии
Секториальный момент инерции (формула 103 [1]):
Изгибо-крутильная характеристика сечения (формула 63 [1]):
Секториальная координата наиболее удаленной точки сечения (Пример 7 [1]):
Крутящий момент:
Изгибно-крутящий бимомент (Приложение 7 [1]):
l – пролет балки
Расчетное напряжение от действия бимомента:
Полное расчетное напряжение от действия изгибающего момента и бимомента:
Сечение балки не удовлетворяет требованиям прочности с коэффициентом использования 1.55.
Проверка результатов ручного расчета на поперечный изгиб с кручением методом конечных элементов в программе ЛИРА 10.
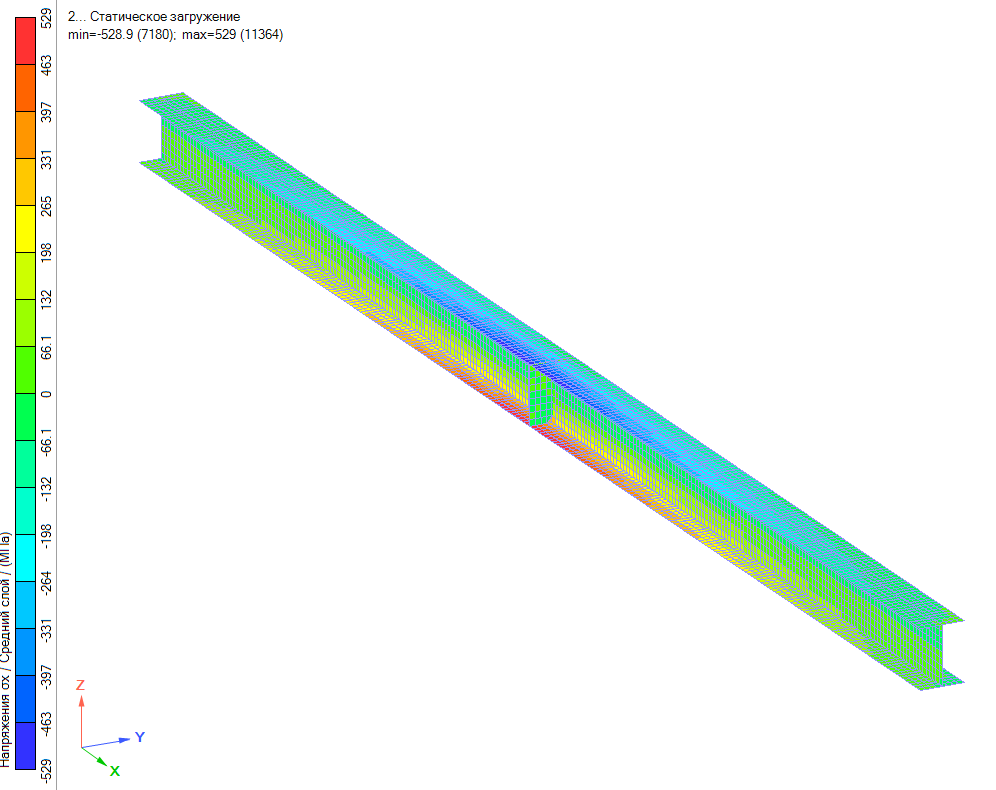Рисунок 5 — Максимальные главные расчетные напряжения в балке 25Ш1
Максимальное напряжение в сечении балки:
Сравнение результатов ручного расчета и расчета в программе ЛИРА 10:
Разница в результатах ручного расчета и расчета в программном комплексе составила 3%.
Выводы и рекомендации
Таблица 3 — Характеристики расчета балки 25Ш1
| Варианты расчета главной балки 25Ш1 | Максимальные расчетные напряжения, МПа |
|---|---|
| Без учета эксцентриситета приложения нагрузки (поперечный изгиб) | 295 - 299 |
| С учетом эксцентриситета приложения нагрузки (поперечный изгиб с кручением) | 529 - 541 |
-
Результаты расчета главной балки 25Ш1 на изгиб с учетом бимомента показали существенное увеличение напряжений (на ~80%) по сравнению с результатами расчета без учета кручения.
-
Учитывая невозможность выполнить проверку на действие бимомента в стержневой расчетной модели в большинстве расчетных комплексов, рекомендуется выполнять ручной расчет по методике [1], либо анализировать напряжения в элементах конструкции, заданных конечными элементами оболочки.
-
Существенный рост напряжений из-за расчетных эксцентриситетов приложения нагрузки на крайние балки перекрытий (покрытий) приводит к значительному увеличению металлоемкости конструкций. В связи с этим рекомендуется конструировать узлы соединений главных и второстепенных балок, исключая возможность возникновения крутящих усилий. На рисунке ниже показан возможный вариант узла с приложением нагрузки на главную балку без эксцентриситета.
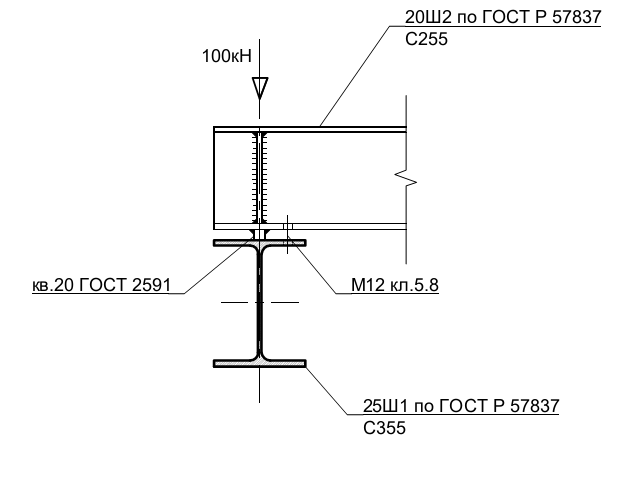Рисунок 6 — Возможный вариант узла с приложением нагрузки на главную балку без эксцентриситета
Список литературы
- Бычков Д.В. «Строительная механика стержневых тонкостенных конструкций - М.: Госстройиздат, 1962.»
